Đường thẳng và mặt phẳng trong không gian

Đối tượng cơ bản của hình học không gian là: Điểm, đường thẳng và mặt phẳng.

Điểm được ký hiệu A, B, C, …

Đường thẳng được ký hiệu a, b, c, d, …

Mặt phẳng được ký hiệu (P), (Q), (R), … hay \((\alpha), (\beta), (\gamma)\)…

Quan hệ cơ bản của hình học không gian:

Thuộc: ký hiệu \(\in\). Ví dụ: A \(\in\) A; M \(\in (\alpha)\).

Chứa trong, nằm trong: ký hiệu \(\subset\). Ví dụ: a \(\subset\) (P), b \(\subset (\beta)\).

Hình biểu diễn của một hình trong không gian

Qui tắc:

Đường thẳng được biểu diễn bởi đường thẳng. Đoạn thẳng được biểu diễn bởi đoạn thẳng.

Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi hai đường thẳng song song (hoặc cắt nhau).

Hai đoạn thẳng song song và bằng nhau được biểu diễn bởi hai đoạn thẳng song song và bằng nhau.

Dùng nét vẽ liền (__) để biểu diễn cho những đường trông thấy và dùng nét đứt đoạn (- – -) để biểu diễn cho những đường bị khuất.

Các tính chất thừa nhận của hình học không gian

Tính chất thừa nhận 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

Tính chất thừa nhận 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

Tính chất thừa nhận 3: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.

Tính chất thừa nhận 4: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

Định nghĩa: Đường thẳng chung của hai mặt phẳng được gọi là giao tuyến của hai mặt phẳng đó.

Tính chất thừa nhận 5: Trong mỗi mặt phẳng, các kết quả đã biết của hình học phẳng đều đúng.

*Định lý:

Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.

Vị trí tương đối của đường thẳng, mặt phẳng

Vị trí tương đối của đường thẳng và mặt phẳng

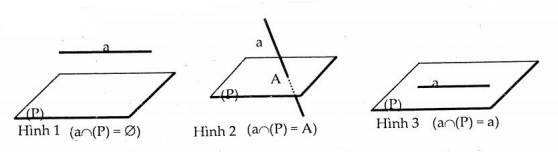
Trong không gian cho đường thẳng a và mặt phẳng (P). Có ba vị trí tương đối giữa a và (P).

a song song với (P) \(\iff\) a và (P) không có điểm chung. Kí hiệu: a // (P) (hình 1).
a cắt (P) \(\iff\) a và (P) có một điểm chung duy nhất, (hình 2).
a chứa trong (P) \(\iff\) a và (P) có hai đểm chung phân biệt.

Kí hiệu: a \(\subset\) (P), khi đó thì mọi điểm thuộc a đều thuộc (P). (hình 3).

Vị trí tương đối của hai mặt phẳng

Trong không gian, cho hai mặt phẳng (P) và (Q).

Có ba vị trí tương đối giữa (P) và (Q).

(P) song song với (Q) \(\iff\) (P) và (Q) không có đường thẳng chung. Khi đó thì (P) và (Q) cũng không có điểm chung. Kí hiệu (P) // (Q). (hình 4)
(P), (Q) cắt nhau \(\iff\) (P) và (Q) có một đường thẳng chung duy nhất. Đường thẳng chung đó gọi là giao tuyến của (P) và (Q). (hình 5).
(P), (Q) trùng nhau \(\iff\) (P) và (Q) có hai đường thẳng chung (hình 6).

Vị trí tương đối của hai đường thẳng

Trong không gian cho hai đường thẳng a, b. Có bốn vị trí tương đối giữa a và b.

a // b \(\iff\) a và b cùng nằm trên một mặt phẳng và không có điểm chung.
a cắt b \(\iff\) a và b có một điểm chung duy nhất.
a = b \(\iff\) a và b có hai điểm chung phân biệt.
a và b chéo nhau \(\iff\) a và b không cùng nằm trên bất kì mặt phẳng nào. Khi đó a và b cũng không có điểm chung.

Chú ý:

Hai đường thẳng cùng chứa trong một mặt phẳng gọi là hai đường thẳng đồng phẳng
Hai đường thẳng cắt nhau hoặc song song là hai đường thẳng đồng phẳng
Hai đường thẳng chéo nhau là hai đường thẳng không đồng phẳng và chúng không có điểm chung

Định lí: Nếu ba mặt phẳng phân biệt cắt nhau từng đôi một và ba giao tuyến của chúng không trùng nhau thì ba giao tuyến đó hoặc song song hoặc đồng quy.

Điều kiện xác định mặt phẳng

1. Ba điểm A,B,C không thẳng hàng xác định một mặt phẳng, kí hiệu mp(ABC).

2. Một đường thẳng d và một điểm A \(\in\) d xác định một mặt phẳng, kí hiệu mp(A,d).

3. Hai đường thẳng cắt nhau a,b xác định một mặt phẳng, kí hiệu mp(a,b).

4. Hai đường thẳng song song xác định một mặt phẳng, kí hiệu mp(a,b).

Hình chóp và hình tứ diện

Hình chóp

Cho đa giác A₁A₂…A_n,nằm trong mặt phẳng \((\alpha)\) và điểm S \(\notin (\alpha)\). Nối S với các đỉnh A₁A₂ ta được n tam giác SA₁A₂, SA₂A₃,…, SA_nA₁. Hình tạo bởi n tam giác đó và đa giác A₁A₂…A_n được gọi là hình chóp. Ký hiệu là S.A₁A₂…A_n.

Tứ diện

Cho bốn điểm không đồng phẳng A, B, C, D.

Hình tạo bởi bốn tam giác ABC, ACD, ADB và BCD được gọi là hình tứ diện.

Các điểm A, B, C, D gọi là đỉnh.

Các đoạn AB, AC, AD, BC, CD và DA gọi là cạnh của tứ diện.

Hai cạnh không đi qua một đỉnh gọi là hai cạnh đối diện.

Các tam giác ABC, ACD, ADB, ABC gọi là các mặt của tứ diện.

Tứ diện có bốn mặt là các tam giác đều được gọi là tứ diện đều.